一粒一粒剥石榴太麻烦？你一定还不知道这个数学原理
原创 Helen 罗博深数学
作者 | Helen
编辑 | 罗数君
文 2367字 阅读时间约 6分钟
导语
相信很多人都被剥石榴深深困扰着，石榴好吃，但剥起来好难！每次搞得满手都是石榴汁，还吃不到几颗。怎么才能轻松吃到石榴？在这篇关于分形几何学的文章里，你一定能发现剥石榴的奥秘！
神奇的分形几何
我记得初中的时候很流行一本书，叫《天才在左疯子在右》。书里面有一章讲到了一个精神分裂以后又痊愈的生物学家，他当时正在研究分形几何学。
书里这样写道：
“简单的举例：比如说随便找一棵树，仔细看一下某枝树杈，你会发现那个分杈和整棵树很像，有些分杈的比例和位置，甚至跟树本身的分杈比例和位置是一样的。如果再测量分杈的分杈的分杈，你会发现同样的现象。假如你直接量叶梗和叶脉，得到的结果还是整棵树分杈的比例。也就是说，树是按照固定的某种模式来生长的；
再说动物，人有五个手指，其实就是微缩了人躯干分出的五个重要分支 —— 双臂，双腿，头；鸟类的爪子也是一样，头，双脚，尾巴。而翅膀平时是收起来的，尾巴却作为了一个肢体末端映射显现出来了。因为收起的翅膀不如尾巴的平衡性重要。这个叫做自相象性。”
当然了，这些现象只是给我们一些最简单的直觉。在数学上，我们说分形是“一个粗糙或零碎的几何形状，可以分成数个部分，且每一部分都（至少近似地）是整体缩小后的形状”。最简单，大家也最熟悉的例子，就是谢尔宾斯基三角形了。
从一个最简单的正三角形开始，我们不断地挖掉中心的小正三角形。就可以源源不断地得到下面的图形。
现在提到分形几何学，我们能想到的，大多数是各种各样绮丽的几何图形。这都要归功于1967年本华·曼德博发表的论文《英国的海岸线有多长？统计自相似和分数维度》。
在这篇文章中，他讨论了海岸线、科赫雪花、皮亚诺曲线这些经典的图形的自相似性。这些图形像巫术一样印在我们脑海里，好像是上帝造物不小心漏出的奥秘。
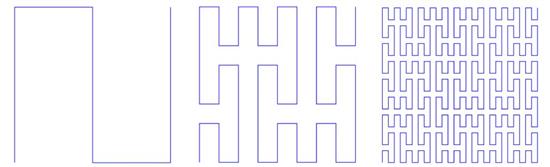皮亚诺曲线
图片来源：wikipedia
科诺曲线
递归实现分形
那么回到最开始，分形几何学究竟是怎样产生的？这都得要从“递归”说起。关注我们公众号的朋友，可能听说过这个词好多次了，大家都知道这是一个基本的计算机术语。那么递归到底是什么？
用简单的语言来说，它是“在函数的定义中使用函数自身的方法。递归一词还较常用于描述以自相似方法重复事物的过程。”
大家小时候央求爸爸妈妈讲故事，一定都听过不耐烦的爸爸妈妈讲的那个偷懒的版本吧？“从前有座山，山里有座庙，庙里有个老和尚，正在给小和尚讲故事。他说：“从前有座山，山里有座庙 …””就是这种被骗的感觉。
这就是递归的感觉。
递归是故事里的故事，函数里的函数。
其实递归的思想最开始并不是为了计算机而产生的，它在数学史上具有非常重要的意义，它是数理逻辑的基石。我在这里按下不谈，相关的逻辑学知识，有兴趣的朋友可以去找书来看看。
言归正传，我们来正式讲一讲递归。
最常见的一个例子，是计算斐波那契数。
我们定义一个函数f, f(n) 能够计算第n个斐波那契数。那我们应该怎么写这个函数？我们知道斐波那契数列的定义是每个数是前两个数字之和。那我们可以说f(n) = f(n-1) + f(n-2)就是我们要的函数吗？
不如举个例子，如果n=5，我们想知道第五个斐波那契是什么。
我们知道这个式子可以一直被分解下去，直到f(1), f(0), 甚至到负数。但是这样一直下去真的有意义吗？我停在了f(0)和f(1), 因为我们知道斐波那契数列的定义是a0 = 0，a1 = 1。计算一下，递归告诉我们，f(5) = 5f(1) + 3f(0) = 5。验证一下，斐波那契数列0，1，1，2，3，5… 第五个斐波那契数确实是5。所以我们定义
f(0) = 0
f(1) = 1
f(n) = = f(n-1) + f(n-2)
作为最后的函数。
你也可以开动脑筋想一想，怎么样用递归的方法，画一个谢尔宾斯基三角形？
用分形几何，
轻松剥石榴！
现在你能体会到递归怎样推动了分形几何学的发展吗？
实际上，分形不仅仅在几何学上有应用，因为它广泛地出现在自然界中，在医学、土力学、地震学和技术分析中都有应用， 在自然、技术、艺术、建筑甚至法律等领域都有出现。尤其是物理学，大家上高中的时候可能听说过布朗运动，也就是分子的热运动。它的轨迹也与分形有关，是随机分形的一种。另外也有关于混沌理论的运用。其涉猎之广，引人遐想。
当然了，这篇文章最重要的还是要交给大家怎样用分形几何学剥石榴。我不知道大家平时是怎么剥石榴的，但是读到分形几何学之前，我被剥石榴深深困扰着。就是觉得石榴特别好看，可是每次剥得不得要领，满手都是石榴汁还吃不到几颗。但在学习分形几何学之后，我发现了剥石榴的奥秘。
首先，请大家看看石榴头顶上的“皇冠”，分形几何学告诉我们，皇冠有多少片“芽”，石榴就有多少瓣。
如果我们把石榴顶摘掉，就能看到石榴内里像橘子一样其实也分了好几瓣儿。要是我们沿着皇冠分割的区域，轻轻地划几刀，把顶摘掉以后，就能像剥橘子一样轻而易举地剥石榴啦。用这个方法剥，不仅手上干干净净，还能确保没有遗漏。
想不到吧？一个简单的剥石榴的过程居然也隐藏着这样神奇的数学奥秘。生活中类似的数学小原理还有很多很多。我在这里抛砖引玉啦，你还能想到更多用分形几何学剥水果的方法吗？在评论区告诉我们吧！
* 本文内容属罗博深数学及其母公司Expii, Inc所有，如需转载请联系罗博深数学团队，未经授权请勿转载。欢迎转发本文与全世界的朋友分享数学、教育的乐趣。原标题：《一粒一粒剥石榴太麻烦？你一定还不知道这个数学原理》
阅读原文
新闻推荐
面对一场突如其来的疫情，在家追剧成为了不少人的选择，这也让在线长视频业务迎来了意料之中的上涨。为此，各大卫视、...