新研究：意法德新冠单日新增高峰或达1.5万、2万、5万
目前，新冠疫情的“震中”已经来了欧美国家。意大利成为重灾区，德国法国情况也不容乐观。
来自法国国家科研中心(CNRS)和美国范德堡大学（Vanderbilt University）的一份最新研究预测，由于意大利、法国、德国的公共干预措施执行较晚，这三个国家的新冠疫情在未来或进一步加重。该研究通过建模预计：意大利新冠疫情高峰发生在4月9日左右，法国4月14日左右，德国5月1日左右。
对这三个国家而言，每天的最大病例数在意大利为10000至15000，在法国为12000至20000，在德国在200000到500000之间。对于这三个国家，如果没有进一步的施加重大公共措施，这些数字很可能会长期维持高位。
而对公共干预措施执行较早的国家韩国来说，新冠疫情的高峰发生在2月29日左右。研究者看到他们的模型与韩国的数据非常吻合。根据研究者的模型，在2月29日的转折点附近，每日病例数最多达到约700例。
以上研究于近日刊发在医学预印本网站medRxiv上。作者P. Magal来自法国国家科研中心(CNRS)。该中心成立于1939年，是法国最大的科学技术研究机构，也是全球最大的基础研究机构。作者G. Webb来自范德堡大学（Vanderbilt University），该学校创立于1873年，是位于美国南方的顶级名校。
论文作者模拟了韩国、意大利、法国和德国的COVID-19流行情况。具体来说，是使用早期报告的病例数据来预测最终报告病例的累计数量。论文作者表示，模型的关键特征是诸如“限制社会流动”这样的公共政策的施行时机，未报告病例的识别、隔离，以及无症状病例的影响。
截至当地时间3月30日18时，意大利24小时新增新冠肺炎确诊病例4050例，累计确诊101739例。
根据法国公共卫生部门当地时间3月30日晚公布的数据显示，法国新冠肺炎确诊病例累计44550例，较前一日增加4376例。
德国疾控机构罗伯特·科赫研究所当地时间3月30日公布的最新数据显示，截至当天8时，德国新冠肺炎确诊病例57298例，较前一日新增4751例。
附：研究方法
该模型的目的是根据早期报告病例数据，预测未来的病例数。模型的焦点是分析遏制流行病的公共政策应用于韩国、意大利、法国和德国的新冠疫情。
在流行的早期阶段，报告的病例数据呈指数增长，这对应的是恒定的传输速率。研究者假设政府的措施和公众开始意识到疫情的严重性，导致这种早期恒定的传输速率改变为“随时间呈指数下降”的速率。
研究者的模型结合了COVID-19流行病的以下基本要素：（1）无症状感染者（有非常轻微或没有症状）的数量，（2）已报告的有症状感染者的数量（症状严重）和（3）未报告的有症状的感染者（症状轻微）的数量。
COVID-19流行病可以分为三个阶段：
第一阶段：报告病例数线性增长，每日报告病例数几乎保持不变；
第二阶段：指数增长阶段，其中病例数呈指数增长，对应于恒定的传播速率。
第三阶段：由于主要的公共干预和社会疏离措施，该流行病的第三阶段对应于时间呈指数递减的传播速度。
研究者的分析将韩国、意大利、法国和德国的流行病确定为第三阶段。
数据
研究者使用来自韩国疾病控制中心，意大利卫生部，法国卫生署和德国罗伯特·科赫研究所的数据。图1给出了累计报告的病例，图2给出了每日报告的病例。
（a）韩国在1月20日至3月9日期间报告的COVID-19病例累计数；（b）意大利在1月31日至3月8日之间报告的COVID-19病例累计数； （c）法国在2月25日至3月9日之间报告COVID-19病例累计数；（d）德国2月24日至3月9日之间报告的COVID-19病例累计数。
（a）韩国在1月20日至3月9日之间每日报告的COVID-19病例数；（b）意大利在1月31日至3月8日之间每日报告的COVID-19病例数；（c）法国在2月25日至3月9日之间每日报告的COVID-19病例数；（d）德国在2月24日至3月9日之间每日报告的COVID-19病例数。
模型
该模型由以下微分方程组组成：
该系统加入了初始数据
这里t≥t0是以天为单位的时间，t0是流行病模型的开始日期，S（t）是在时间t易受感染的个体数，I（t）是在时间t的无症状的传染性个体数t，R（t）是在时间t的已报告症状传染病个体的数量，U（t）是在时间t的未报告症状传染病个体的数量。
在时间t的传播速率是τ（t）。无症状感染者I（t）的平均感染期为1 / v天。报告的有症状的个体R（t）的平均感染时间为1 /η天，未报告的有症状的个体U（t）也是如此。研究者假设：已报告的有症状感染者R（t）会立即分离出来隔离，并且不会引起进一步的感染。无症状个体I（t）也可以被视为具有低水平的症状状态。所有感染均来自I（t）或U（t）个体。无症状感染的分数f成为有症状的传染病，而1- f的分数未报告有症状的传染病。无症状传染病症状报告率是ν1= fν，无症状传染病症状报告率是v2 =（1 ? f）ν，其中ν1+ν2=ν。在时间t的累计报告病例数由公式给出：
且在时间t处未报告的累积数量由公式给出
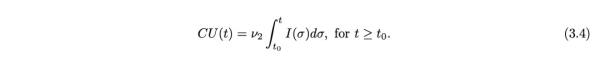
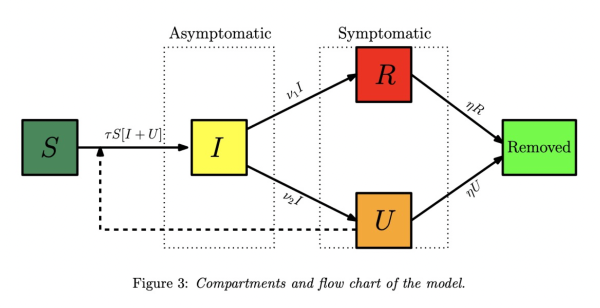表1：模型的参数和初始条件。
参数估计方法
研究者假设f = 0.6或f = 0.1，这意味着40％或90％的有症状感染病例未报告。f的实际值未知。研究假设η= 1/7，这意味着未报告的有症状感染者和报告的有症状感染者的平均感染期为7天。研究者假设ν= 1/7，这意味着无症状感染者的平均感染期为7天。随着进一步流行病学信息的了解，可以修改这些值。
研究者假设在COVID-19流行的第二阶段，根据以下公式，已报告病例的累计发生率CR（t）大约呈指数增长：
研究者确定值χ3=1。当认识到CR（t）呈指数增长时（即研究者使用指数拟合χ1exp），将χ1和χ2的值拟合到流行病初期的累积报告病例数据。 （χ2t）以拟合数据CR（t）+ 1）。研究者假设初始值S0对应于所报告病例数据区域的总体。假定通过去除第二阶段开始时的感染人数，易感人群S（t）的值仅略有变化。其他初始条件是：
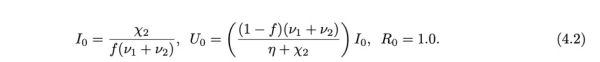在流行的第二阶段，当报告病例的累计数量呈指数增长时，传播速率τ（t）的值是恒定值：
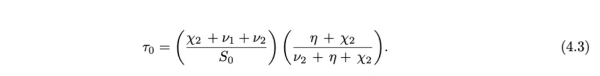早期指数增长阶段开始的初始时间是：
基本传染数R0为：
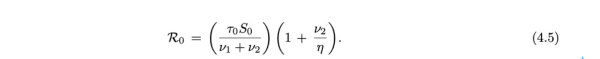I0，U0，t0，τ0和R0的这些公式是在[1]中得出的。 从技术上讲，它们的数值对于确定第二阶段CR（t）的指数增长率至关重要。
在第二阶段，τ（t）≡τ0恒定。当实施强有力的政府措施（例如隔离，检疫和公共关门）时，第三阶段开始。这些措施的实际效果是复杂的，并且在第三阶段中，研究者使用指数减小来降低随时间变化的传输速率τ（t），以纳入这些效果。第三阶段的τ（t）的公式为：
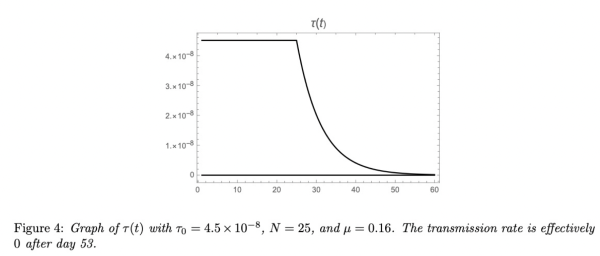
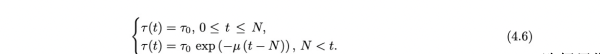选择日期N和μ的值，以使流行病数值模拟中的累计报告病例与第N天后公共措施生效时的累计报告病例数据一致。这样，研究者就可以在政府施加公共限制措施生效后，预测流行病的时间路径。研究者在图3中说明了典型情况下的τ（t）。
通过计算以下方程式的解，可以得出该模型每天报告的病例数：
预测病例总数：
在本节中，研究者将第4节中描述的方法应用于来自韩国、意大利，法国和德国的数据。在表2中，研究者选择（1）韩国2月19日至2月30日的数据；（2）意大利2月21日至3月3日的数据；（3）法国2月25日至3月7日的数据；（4）德国2月24日至3月6日的数据。
预测韩国的病例数：
预测意大利的病例数：
预测法国的病例数：
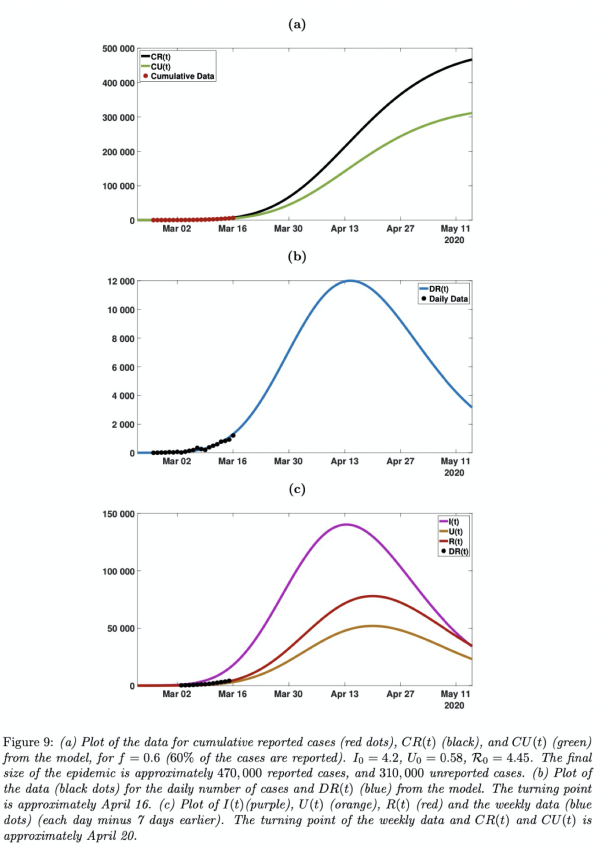
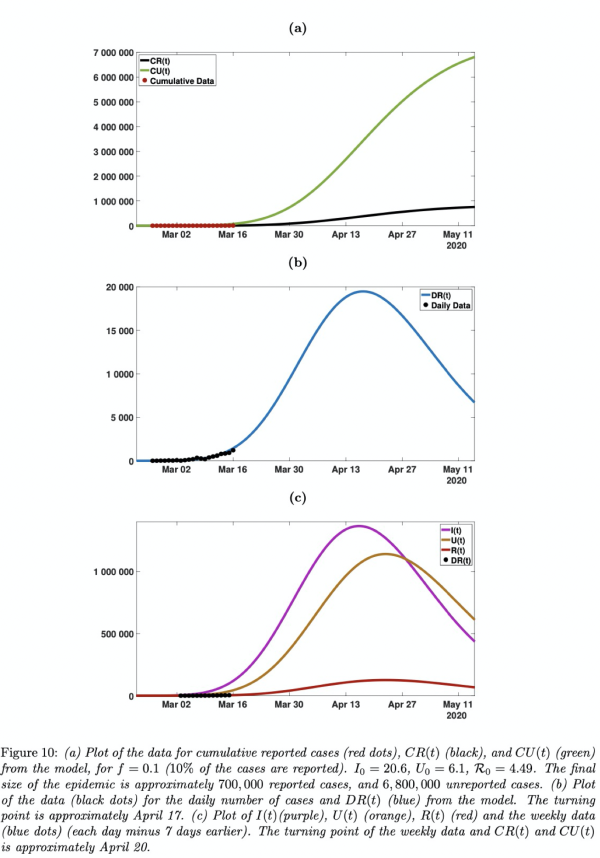预测德国的病例数：
结论：
研究者根据在一个地区已经报道的病例数据，应用之前开发的方法来预测该地区的新冠流行病演变。当流行病处于第二阶段并呈指数增长时，拥有恒定的传播速率时，研究者将早期数据深入模型中。当政府开始采取公共措施以遏制流行病时，第三阶段就开始了，此时研究者以随时间呈指数递减的传输速率进行建模。研究者此前将这种方法应用于中国大陆，并证明了研究者的模型能够预测该流行病的进程。
在本研究中，研究者使用累计报告病例数，每日报告病例数和四个国家每周报告的病例数。借助这些数据，研究者可以预测每个国家/地区未来报告和未报告的病例数。研究者假设未报告的病例占总数的f。研究者模拟每个国家的f = 0.6和f = 0.1的模型。分数f = 0.6和f = 0.1分别对应于较小和较大的最终尺寸。对于韩国来说，由于采取了限制公众的社交距离等重大措施，疫情已经消退。在意大利，法国和德国，新冠疫情仍在上升，因为这些措施是最近才实施的。
研究者的模型在第三阶段通过与时间有关的传输速率τ（t）纳入了社会距离疏远措施。该速率涉及μ（与这些度量相对应的指数衰减率）和N（它们生效之日）。显然，这些措施应尽早开始，并应尽可能强大。后期公共干预的后果可能会对疫情造成严重后果。
以韩国为例，新冠疫情的高峰发生在2月29日左右。在图5和6中，研究者看到研究者的模型与韩国的数据非常吻合。根据研究者的模型，在2月29日的转折点附近，每日病例数最多达到约700例。
与韩国相比，意大利，法国和德国的公共政策干预相对较晚。研究者预测：新冠疫情高峰发生在意大利的4月9日左右，法国的4月14日左右和德国的5月1日左右。每天的最大病例数在意大利为10000至15000，在法国为12000至20000，在德国在200000到500000之间。对于这三个国家，如果没有进一步的重大公共措施，这些数字很可能会长期维持高(本文来自澎湃新闻，更多原创资讯请下载“澎湃新闻”APP)
新闻推荐
原创小鹿LicorneUnique新艺术大师穆夏与塞西斯联手出品雕塑《百合女神》19世纪末，蒸汽机的轰鸣取代了教堂的钟声，人们迎来...